Numerous studies have identified that topography significantly influences the amplification of seismic waves, with amplifications occurring on convex forms such as hills and deamplification on concave geoforms such as valleys and canyons (Rai, 2015)
Calibrating the model is essential for ensuring its reliability. A close correspondence between the modeled results and actual earthquake measurements validates the model’s accuracy (@#fig-stations). Below is another numerical model from Pereira, Colombia, where the impact of topography on amplification is clearly visible. Most importantly, this example underscores the precision of the two-dimensional model in capturing these effects.
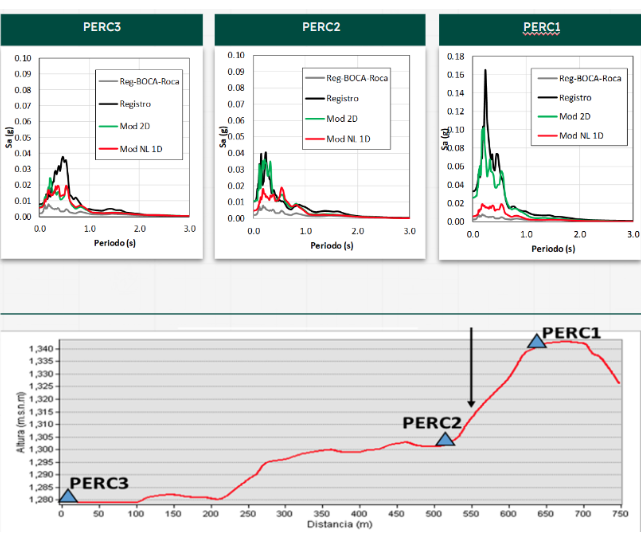
PERC1, PERC2, and PERC3 are accelerometer stations located on varying topographies. Each figure presented includes four lines representing different aspects of seismic data analysis:
Reg-Boca-Roca (gray line) illustrates the actual signal recorded over rock ( Vs > 760 m/s), which was used as the input signal
Mod NL 1D (red line) illustrates the response spectrum generated by a one-dimensional model.
Mod 2D (green line) illustrates the response spectrum generated by a two-dimensional model.
Record (black line) illustrates the response spectrum from a real earthquake event
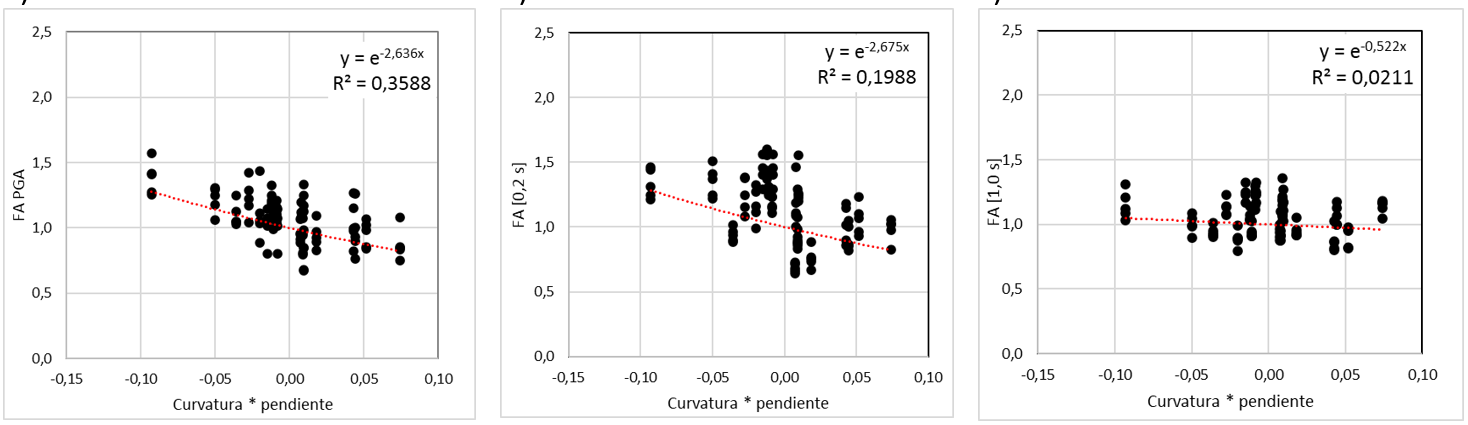
I conducted several two-dimensional models across a range of intensities, selecting multiple points on the surface to compute curvature and slope from a digital elevation model. These calculations were then correlated with amplifications, enabling me to establish functional relationships. These relationships illustrate how terrain characteristics influence amplification effects for specific spectral periods (PGA, 0.2 s, 1.0 s) (Figure 2).
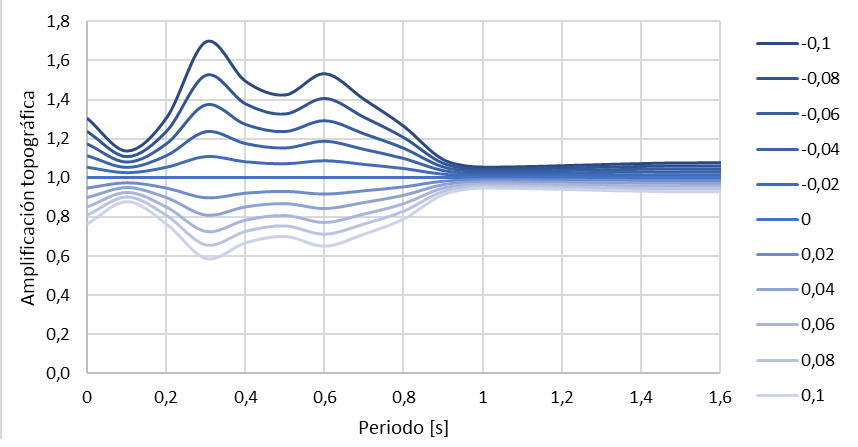
In Figure 3, we observe transfer functions corresponding to each combination of slope and curvature. It’s evident that a curvature of zero results in an amplification equal to zero. Positive curvatures represent crests, leading to amplifications, while negative curvatures are indicative of valleys, resulting in deamplifications.
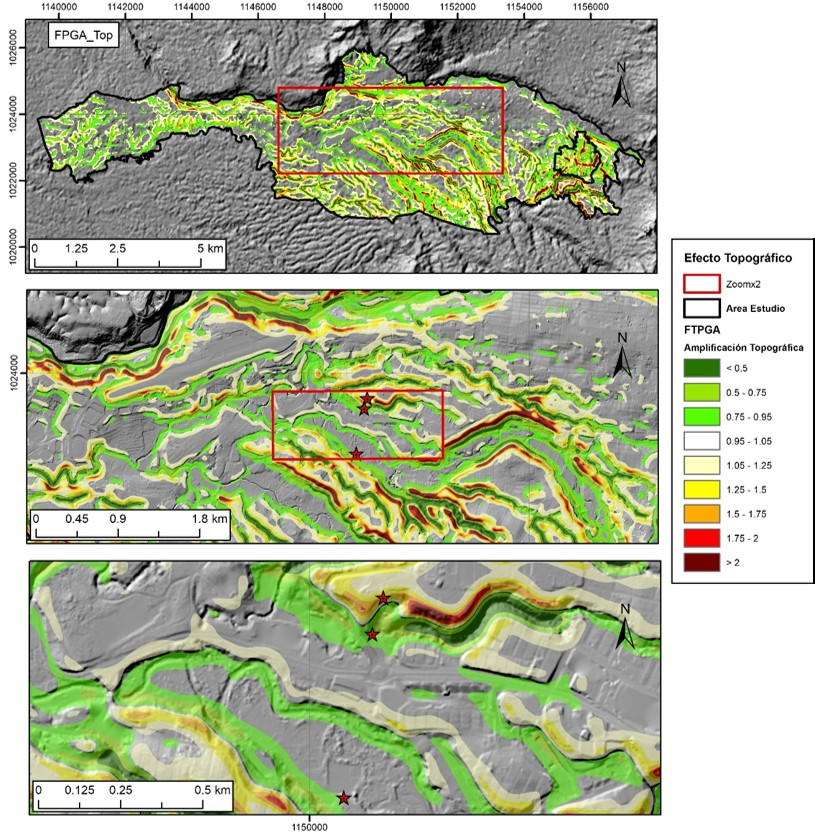
To effectively integrate the amplification function into building codes, thereby enhancing seismic risk assessment and informing policy development, the calculated amplification (as shown in Figure 3) across various curvature-slope combinations is spatially mapped out in Figure 4 for a fixed spectral period. This approach allows for a detailed visualization of how topographic features influence seismic amplification, offering valuable insights into the spatial variability of seismic risk. By delineating areas of high amplification, this spatialization aids in the targeted refinement of building codes, ensuring that structures are designed with an optimal level of resilience against seismic forces specific to their topographic setting.